‘Anomalous weak values’ are nonclassical, and here is the proof

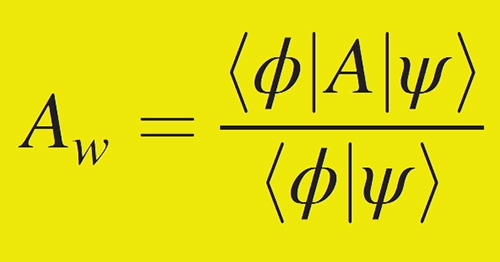
The weak value of an observable A can be nonsensical.

By Hamish Johnston

Last month we reported on a quirky paper in Physical Review Letters entitled “How the result of a single coin toss can turn out to be 100 heads” by Christopher Ferrie of the University of New Mexico and Joshua Combes of the Perimeter Institute for Theoretical Physics in Waterloo, Canada.

The paper addresses “anomalous weak values” in quantum mechanics, a phenomenon that was first identified in 1988 by Yakir Aharonov, Lev Vaidman and colleagues at Tel Aviv University. A weak value is the result of a weak measurement on a quantum system. This is done by making repeated gentle measurements on the quantum states of identical particles. The result of each measurement only has a tiny correlation to the quantum state of the particle so the wave function of the particle does not collapse into that state. However, by making the measurement on many particles, a weak value providing useful information about the state can be obtained.

The problem is that sometimes the weak values can seem absurd. In 1988 Aharonov and colleagues showed that weak measurement of the spin of a spin-½ particle can result in a weak value of 100, which is 50 times greater than the largest possible value of the spin, which is of course ½.

The existence of such anomalous weak values is considered by some physicists to be yet another paradox of quantum mechanics. Others, including Ferrie and Combes, have questioned whether they are quantum effects at all. Indeed, in their paper the duo shows that such values can easily arise in a simple coin-flipping experiment with no reference to quantum mechanics.

Now, Matthew Pusey of the Perimeter Institute has published a paper in Physical Review Letters in which he offers a proof that “anomalous weak values are nonclassical in a precise sense”. I believe that he is arguing that in a quantum system (and not in a coin-flipping analogue!) such weak values are a result of quantum mechanics.

The paper is called “Anomalous weak values are proofs of contextuality”, and if you want to know more you will have to read it yourself. The mathematics is way over my head!

You can also discover much more about weak measurements in “In praise of weakness” by Aephraim Steinberg, Amir Feizpour, Lee Rozema, Dylan Mahler and Alex Hayat at University of Toronto.